1. 引言
在DT时代,挖掘海量数据并从中提炼出有价值的信息是各大互联网公司的重要目标之一。在拥有海量数据后,各种各样的数据挖掘任务就出现了,大规模稀疏矩阵相乘就是其中一项常见的计算任务。在文本处理或者说自然语言处理中,稀疏矩阵是常见的数据表达形式,对大规模稀疏矩阵做乘法的业务需求也是很常见,比如:
- 现有大量的object(比如数千万甚至更大的规模),已通过某种特征抽取算法建立起每个object的稀疏特征向量,这里object可以是query、word、URL、host、APP、商品、用户等,现在有个任务是对每个object找出与其相似的object。在个性化推荐领域中经常碰到这类问题。
- 现有第1份数据是每个用户浏览的URL列表,每个URL带有权重分数,第2份数据是query到URL的搜索点击关系,每个URL也带有权重分数,用户规模、query规模、URL的规模均在数千万的规模,现在有个任务是给每个用户找出一批合适的query来描述。
- 现有第1份数据是每个用户浏览的商品ID列表,每个商品ID带有权重分数,第2份数据是query到商品ID的搜索点击关系,每个商品ID也带有权重分数,用户规模、query规模、商品ID的规模均在数千万的规模,现在有个任务是给每个用户找出一批合适的query来描述。(这里,query也可以变成是商品的核心词)
- 已有一份词典D,其对每个query列举了与其相似query和相似性分数,左侧query的规模在数千万的规模。但是其中有些query的相似query列表较短,如果需要扩展列表,一种办法是通过把相似的query拿到字典D中再查询一次,以丰富query的相似query列表内容。
上述例子还只是大规模稀疏矩阵相乘任务的冰山一角,还有更多的业务场景需要用到它。既然需要大规模稀疏矩阵相乘的任务很多,那么有必要对该任务研发出一套scalable的通用分布式计算工具。笔者刚好在最近的一些工作中碰到了这类需求,就基于MapReduce开发了一套工具以支持团队需求。
下文就针对单机不能处理,需要用到分布式计算平台(比如MapReduce)的大规模矩阵相乘问题,列举研发此工具的一些经验教训。先简单介绍适用于稠密矩阵的矩阵相乘算法,然后介绍适用于稀疏矩阵的矩阵相乘算法,继而介绍工程实现上的一些trick,最后简单做个总结。笔者了解的东西不多,欢迎各位读者批评指正。
2. 矩阵相乘的形式化定义
将一个\(m \times n\)的矩阵A和一个\(n \times k\)的矩阵B相乘得到\(m \times k\)的矩阵C,数学公式如下:
\begin{equation}\mathbf{C}_{x,\ y} = \displaystyle\sum_{i=0}^{n-1} {\mathbf{A}_{x,\ i} \times \mathbf{B}_{i,\ y}}\end{equation}
下面考虑的是A和B都是大矩阵的情形,即单机计算时间很长甚至是单机无法加载数据,这时只能依靠分布式计算平台(比如MapReduce)。从公式1可以看出,A和B的每个元素都被用于计算C中不止一个元素的值,整个计算复杂度是 \(\mathbf{O}(m \times n \times k)\),如果m、n、k均为百万量级,那么计算复杂度就在\(\mathrm{10}^{\mathrm{18}}\)的量级,这样的计算规模是相当大的。当今主流CPU的每秒处理速度在\(\mathrm{10}^{\mathrm{9}}\)量级,所以靠暴力求解法并不合适。研发一款实用的大矩阵相乘工具是很有必要的,要考虑计算精度、计算速度、shuffle数据量和数据倾斜等情况。
3. 适用于稠密矩阵的矩阵相乘算法
3.1 简单相乘法
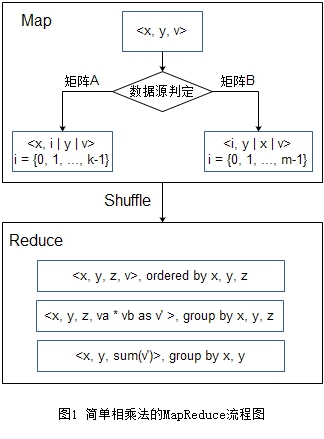
简单相乘法可谓是最朴素的MapReduce上矩阵相乘算法,用此方法作为算法比较的基础。简单相乘法依据公式(1)来实现矩阵乘法,图1是其算法流程图。图中,Map输出的第一个”|”表示分桶 key的位置,第二个”|”表示排序 key的位置。它只需要一轮MapReduce。
Map阶段每读入一条数据\(<x, y, v>\),需要输出若干条数据。若它来自于矩阵A,则需要输出k条数据,需输出\(<x, i, y, v>, i = \{0, 1, …, k - 1\}\),补充说明,\(x \in \{0, 1, …, m - 1\}, y \in \{0, 1, …, n - 1\}\);若它来自矩阵B,则需要输出m条数据,需输出\(<i, y, x, v>, i = \{0, 1, …, m - 1\}\),补充说明,\(x \in \{0, 1, …, n - 1\}, y \in \{0, 1, …, k - 1\}\)。前两个字段为分桶key,前三个字段为排序key。Reduce 阶段的输入是\(<x, y, z, v>\),当且仅当前后两条输入数据的x, y, z均相同时,说明 A 中存在A[x][z],B中存在B[z][y],应该把它们俩的值相乘累加到C[x][y]。由于是按x, y分桶并按x, y, z排序,所有能贡献到C[x][y]的数据都分配到这个reducer并排列在一起,因此当目前读取的x, y与上一个不同时,若上一个x, y累加的sum不为0,则输出\(<x, y, sum>\)。
矩阵A和矩阵B中的每个元素要发送多次,总的网络传输数据量,也就是shuffle数据量,是\(\mathbf{O}(m \times n \times k)\)。对大规模矩阵,m, n, k都是较大的数(比如这3个数均在数百万的量级,则传输规模在\(\mathrm{10}^{\mathrm{18}}\)量级),这种情形下的网络传输量会特别大。当矩阵稀疏时,大部分 A发送的数据找不到与 B 发送的x, y, z相同且非零的数据,反之亦然,因此有很多网络传输是浪费的。可见这个算法对于稀疏矩阵乘法并不高效。
3.2 分块相乘法
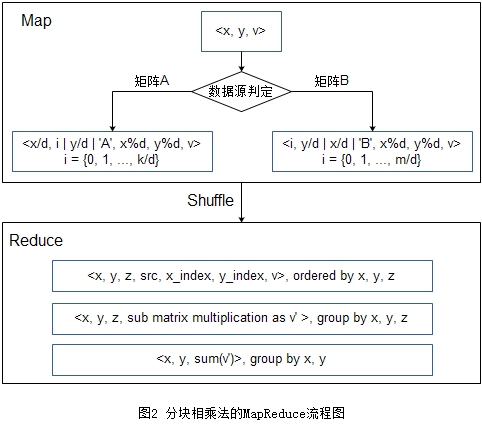
分块相乘法,也就是在线性代数或者矩阵论教材上所说的分块矩阵相乘法,该方法有点类似于递归思路,即把原问题的求解先分解为多个子问题的求解,然后在做某种恰当的归并操作。分块相乘法有多种具体实现,这里举一种代表性的实现方案,很多方法可以视为该方法的变种。图2是一种实现方案。图中,Map输出的第一个”|”表示分桶 key的位置,第二个”|”表示排序 key的位置。它也只需要一轮MapReduce。
将矩阵A和矩阵B都分成大小为\(d \times d\)的块。这样矩阵A的行被分成了\(\lceil m/d \rceil\)块,列被分成了\(\lceil n/d \rceil\),子块的行下标取值范围为\(\{0, 1, …, \lceil m/d \rceil - 1\}\),列下标取值范围为\(\{0, 1, …, \lceil n/d \rceil - 1\}\)。矩阵B的行被分成了\(\lceil n/d \rceil\)块,列被分成了\(\lceil k/d \rceil\),子块的行下标取值范围为\(\{0, 1, …, \lceil n/d \rceil - 1\}\),列下标取值范围为\(\{0, 1, …, \lceil k/d \rceil - 1\}\)。下文为了表达简洁,用\(x/y\)表示\(\lceil x/y - 1 \rceil\)。Map阶段每读入一条数据\(<x,y,v>\),需要输出若干条数据。若它来自于矩阵A,则需要输出\(k/d\)条数据,需输出\(<x/d, i, y/d, 'A', x\%d, y\%d, v>, i=\{0, 1, …, k/d\}\),补充说明,\(x \in \{0, 1, …, m - 1\}, y \in \{0, 1, …, n - 1\}\);若它来自矩阵B,则需要输出\(m/d\)条数据,需输出\(<i, y/d, x/d, 'B', x\%d, y\%d, v>, i = \{0, 1, …, m/d\}\),补充说明,\(x \in \{0, 1, …, n - 1\}, y \in \{0, 1, …, k - 1\}\)。前两个字段为分桶key,前三个字段为排序key。Reduce 阶段的输入是\(<x, y, z, src, x_{index}, y_{index}, v>\),其中src表示来源,取值'A'或者'B',\(<'A', x_{index}, y_{index}, v>\)的list构成来自矩阵A的子块,\(<'B', x_{index}, y_{index}, v>\)的list构成来自矩阵B的子块。当且仅当前后两条输入数据的x, y, z均相同时,说明 A 中存在子块A[x][z],B中存在子块B[z][y],应该把它们两矩阵相乘的结果累加到子块C[x][y]。由于是按x, y分桶并按x, y, z排序,所有能贡献到C[x][y]的数据都分配到这个reducer并排列在一起,因此当目前读取的x, y与上一个不同时,则输出\(<x, y, sum\_matrix\_multiplication>\)。
用分块相乘法进行矩阵相乘最大的优点是每条数据只会被发送\(k/d\)次,大大降低了网络通信。在设置d的大小时有一个限制,在本地相乘的2个子块占用的空间\(\mathbf{O}(d^2)\)不会超过机器的内存限制。
此方法有诸多变种,可以总结为2类思路,一类是子块大小不设置成\(d \times d\)和矩阵B的大小规模来配置;一类是优化算法,提高计算性能。对稀疏矩阵,有可能划分出两个为空的子块进行相乘,此时传输这两个块的开销仍是不必要的。虽然有方法对此进行优化,但由于矩阵稀疏,还会碰到两个不为空的子块相乘,结果为空的情形,此时传输这两个块的开销仍是浪费的。
4. 适用于稀疏矩阵的矩阵相乘算法
4.1 矩阵相乘的向量表达形式
公式1还可以用向量的形式来表达,如公式2所示,其与公式1是等价的。
\begin{equation}\mathbf{C} = \displaystyle\sum_{i=0}^{n-1} {\mathbf{A}_{\cdot,\ i} \times \mathbf{B}_{i,\ \cdot}}\end{equation}
A的列向量有n个,B的行向量也有n个,将A的某个列向量与B的对应行向量相乘,得到\(m \times k\)的中间结果矩阵,将这n个中间结果矩阵相加,即得到结果矩阵C。公式2表面上看似抽象,但放到具体的业务中,其实有很强的物理意义。举个例子(就用第1节中的第2个例子):现有第1份数据是每个用户浏览的URL列表,每个URL带有权重分数,第2份数据是query到URL的搜索点击关系,每个URL也带有权重分数,用户规模、query规模、URL的规模均在数千万的规模,现在有个任务是给每个用户找出一批合适的query来描述。对这个问题,矩阵A的m是全部的user,n是全部的URL;矩阵B的n是全部的URL,k是全部的搜索query。公式2的意思就是说:对某个URL而言,将其对应的user向量与query向量进行相乘,得到一个user到query的中间结果矩阵C’,维度是\(m \times k\)。遍历全部的URL,将得到的各个中间结果矩阵C’相加即可得到矩阵C。通过这样一个解释能看到,作为索引项的URL其实是从user到query这种联系的桥梁。
对于稀疏矩阵,某个URL对应的user向量和query向量有很多是零值,这些零值元素对计算出最终的矩阵C没有任何数值上的贡献。如果不是直接用公式2计算,而是建立URL到user和URL到query的倒排索引,并且只索引非零值。这样就可以进一步化简问题,也就引发出基于倒排索引的稀疏矩阵乘法。
4.2 单侧倒排索引的矩阵相乘法
如果矩阵A和矩阵B中存在一个矩阵较小(比如矩阵的行数是十万这种量级,各行平均包含的非零值个数是数百这种量级),其倒排索引的空间开销小于MapReduce集群对节点的内存限制(不少公司的Hadoop集群要求各计算任务的节点内存开销在2G以内)。不失一般性,假设是矩阵A的倒排索引能被单节点加载,算法需要1轮MapReduce,且只需map阶段。Map阶段将矩阵A建立倒排索引,矩阵B按行切分将数据分配到不同的Map节点上,各节点每读入一条\(<x,y,v>\),执行类似搜索引擎检索的流程,从倒排链中拉取出与其相关的全部的A中元素,并相应的计算出向量点积。
当存在部分倒排链特别长时,可以将这些倒链再split成几个子倒链(计算精确无损),也可以设置一些cutoff值,比如倒链最大长度、倒链元素分数的最低阈值等(计算精度有损)。
4.3 双侧倒排索引的矩阵相乘法
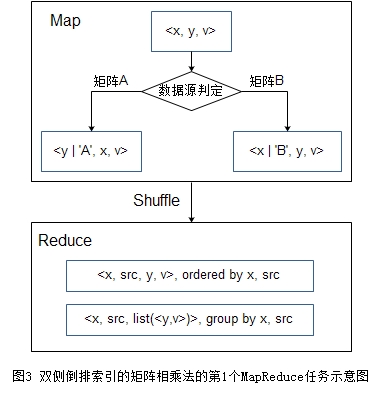
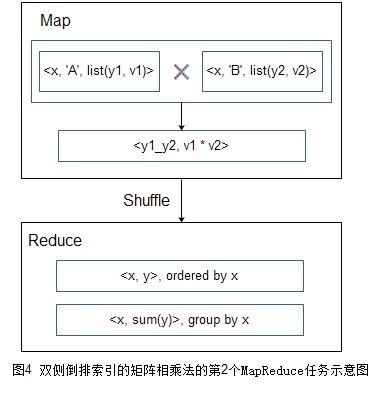
当矩阵A和矩阵B都较大,无论哪边的索引都超过MapReduce集群对节点的内存限制,那么就需要对两矩阵都建立倒排。如上文所说,当输入矩阵的某个\(<x,y>\)的v为0,因为零值元素对矩阵相乘的最终结果不会有分数上的贡献,所以不用将该项加入到索引中。在充分利用稀疏矩阵的这一特性后,我们可以设计出高效的矩阵相乘法。图3和图4是算法的2轮MapReduce的流程图。
第一轮 Map阶段将矩阵A按列划分,矩阵B按行划分,即每读入一条\(<x,y,v>\), 若来自矩阵 A, 则输出\(<y,'A',x,v>\);若来自矩阵B,则输出\(<x,'B',y,v>\)。以第一个字段为分桶 key,前两个字段为排序 key。这样A的第i列和B的第i行会被发送到同一个reducer并放在一起,而且A的数据在前,B的数据在后。这样Reduce阶段就先输出i索引到A的数据,后输出同一个i索引到B的数据。
第二轮Map阶段对每个i,对索引到A的数据集合和索引到B的数据集合求笛卡尔积,并把y1_y2组合作为key,其分数乘积\(v1 \times v2\)作为value发送给reducer,Reduce阶段只需要将第一轮输出中相同key的值求和。
为了更方便的理解流程,下面对具体的例子(还是用第1节中的第2个例子)给出算法流程图,请见图5和图6。第1轮建立起关于URL的倒排索引,第2轮Map阶段对倒排索引的各项计算笛卡尔积,然后Reduce阶段对相同key进行求和。
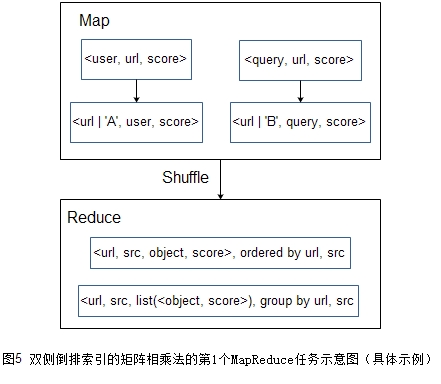
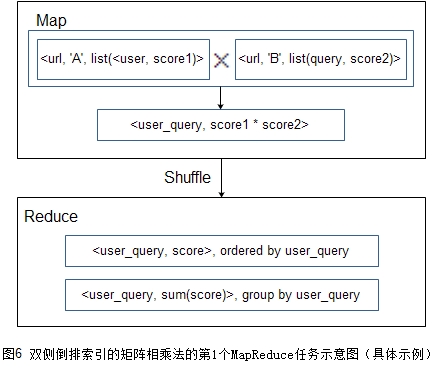
考虑到MapReduce集群对节点的内存限制,使用这种方法要注意各单项元素的倒排链不能太长,如果每个索引项需要的存储空间为100字节,那么可以估算倒排链长度的极限是\(\mathrm{10}^{\mathrm{7}}\),也就是1000万。为稳定运行该流程,建议控制在数百万的量级。另外,在实际业务中,如果某元素的倒排链长度能到100万甚至更多,那一般来说此元素其实价值不大。比如,某URL能被100多万用户访问,这一方面说明此URL是高频URL,但另一方面也说明此URL的信息量不大,用此URL去架起user到query的桥梁的意义不大,从业务层面上看,这样的URL是可以被舍弃的。
4.4 双侧倒排索引的矩阵相乘法的工程实现trick
分析双侧倒排索引的矩阵相乘法的流程,容易发现瓶颈会存在于第2轮MapReduce中,具体是map节点把进行笛卡尔积运算后的结果发送给reduce节点。假设关于矩阵A和关于矩阵B的倒排链的平均长度分别为p和q,那么单个索引项带来的笛卡尔积的计算复杂度为\(\mathbf{O}(p \times q)\),因为一共有n个索引项,所以总的计算复杂度为\(\mathbf{O}(n \times p \times q)\),因为矩阵是稀疏的,所以这里\(p<<m,q<<k\)。比如m、n、k均为百万量级,但p和q是在一万这种量级,那么计算复杂度就在\(\mathrm{10}^{\mathrm{14}}\)的量级,虽然比原先的\(\mathrm{10}^{\mathrm{18}}\)的量级小了很多,但这个计算复杂度还是大,CPU开销和网络IO开销均是在\(O(n \times p \times q)\)量级。由此可见,笛卡尔积的计算是这个算法性能的关键点。
\(O(n \times p \times q)\)量级的计算代价是精确计算、没有精度损失情况下的计算代价。不过一些实际业务是允许有精度损失的。比如对第1节中的第2个例子,当只需要对每个用户找到最合适的top N的query,那么可以对倒排链做些恰当的剪枝操作。剪枝策略主要是设置一些cutoff值,比如倒链最大长度、倒链元素分数的最低阈值等。
在工程实现上,还要考虑数据倾斜的问题。在很多互联网业务中,数据均服从幂律分布。比如存在部分URL会对应到特别多的用户或者query,但这部分URL的数量在全部URL中的占比不大。为了缓和数据倾斜,可以在第1轮MapReduce的Reduce阶段加入长倒链切分成若干个短倒链的逻辑,并多加入一轮针对倒链数据的shuffle的MapReduce操作。这种方案并不会带来精度损失,但会提高后面算笛卡尔积的MapReduce任务的计算效率。在笔者负责的一项业务中,加入这个策略,算笛卡尔积的MapReduce任务的计算时间缩短为原先的1/3。
5. 总结
- 对于稠密矩阵的矩阵相乘,视矩阵大小,来判断使用简单相乘法还是分块相乘法。
- 对于稀疏矩阵的矩阵相乘,视矩阵大小,来判断使用单侧倒排索引的矩阵相乘法还是双侧倒排索引的矩阵相乘法。当然如果已有双侧倒排索引的矩阵相乘工具,那么无论矩阵大小,都可以直接使上。
- 数据稀疏是个好特性,它给算法设计带来特别的考虑。矩阵相乘问题是在计算精度与计算效率上权衡的一个问题,如果实际业务允许一些精度损失,那么可以适当加些剪枝策略以提高计算效率。
原创文章,转载请注明:转载自vividfree的博客
本文链接地址:使用 MapReduce 实现大规模稀疏矩阵相乘